¿QUE ES CIRCUNFERENCIA?
Dispóngase del círculo, que es el lugar geométrico de los puntos contenidos en el interior de dicha circunferencia, o sea, la circunferencia es el perímetro del círculo. Los puntos de la circunferencia están a una distancia igual al radio del centro del círculo, mientras los demás puntos del círculo están a menor distancia que el radio.
10 EJERCICIOS Y PROBLEMAS SOBRE CIRCUNFERENCIA
1
Escribir la ecuación de la circunferencia de centro (3, 4) y radio 2.



2
Dada la circunferencia de ecuación x2 + y2 − 2x + 4y − 4 = 0, hallar el centro y el radio.


3
Calcula la ecuación de la circunferencia que tiene su centro en (2, −3) y es tangente al eje de abscisas.
4
Calcula la ecuación de la circunferencia que tiene su centro en (−1, 4) y es tangente al eje de ordenadas.
5
Calcula la ecuación de la circunferencia que tiene su centro en el punto de intersección de la rectas x + 3y + 3 = 0, x + y + 1 = 0, y su radio es igual a 5.
6
Hallar la ecuación de la circunferencia concéntrica con la ecuación  , y que pasa por el punto (−3, 4).
, y que pasa por el punto (−3, 4).
 , y que pasa por el punto (−3, 4).
, y que pasa por el punto (−3, 4).7
Hallar la ecuación de la circunferencia que tiene el centro en el punto C(3, 1) y es tangente a la recta: 3x − 4y + 5 = 0.
8
Hallar la ecuación de la circunferencia que pasa por los puntos A(2, 0), B(2, 3), C(1, 3).
9
Hallar la ecuación de la circunferencia circunscrita al triángulo de vértices:A(0, 0), B(3, 1), C(5, 7).
10
Hallar la ecuación de la circunferencia que pasa por los puntos A(2, 1) y B(−2, 3) y tiene su centro sobre la recta: x + y + 4 = 0.
¿QUE ES CIRCULO?
Un círculo, en geometría, es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio. En otras palabras, es la región del plano delimitada por una circunferencia y que posee un área definida.En castellano, la palabra círculo tiene varias acepciones, y a veces se utiliza indistintamente círculo por circunferencia siendo esta última una curva geométrica plana, cerrada, cuyos puntos son equidistantes del centro, y sólo posee longitud (es decir, el perímetro del círculo)."Aunque ambos conceptos están relacionados, no debe confundirse la circunferencia (línea curva) con el círculo (superficie)
5 EJEMPLOS DE CIRCULO

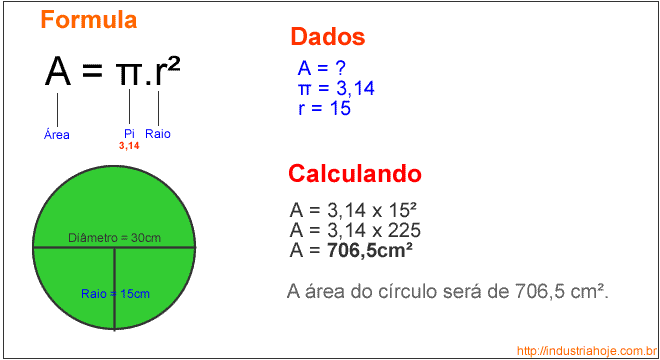






































 QUE ES CIRCULO
QUE ES CIRCULO





























